《Deep Residual Learning for Image Recogn

朋友们从本周开始我会着手更新新系列的博客，论文解析系列。当然此系列我会尽力细致地介绍论文，不过因为水平有限，难免会有理解不到位甚至错误的地方，因此欢迎评论探讨。同时本系列更趋向于介绍论文大致思想，对于论文中太细的小细节便不再做更多介绍，若是大家想更加详细地了解一篇论文的话，还是去看英文原版的吧。但若是想快速了解论文思想和梗概或是不一样的读者想法，大概看看我的博客也不错。欢迎大家评论区留言提建议。

第一篇先拿开刀了，这篇文章想来是近年来deep 领域最有名的文章了吧， best paper，为之后几年的很多研究打下了基础。这一篇文章可以说写的是非常好啊，逻辑清晰且通俗易懂。同时这个新的网络结构思路也是天马行空惊为天人。恺明酱现在好像去了。话不多说，进入正题：

《Deep for Image 》

：

事情的起因在于越深的网络越难以训练，因此作者提出了残差网络。在数据集上，作者使用了152层的残差网络进行训练，比VGG网络深了8倍，但是复杂度却更低。同时精度取得了第一。

：

首先，作者抛出观点，随着网络层数的加深，网络的表达能力会更强，这已经被很多研究所证实。与此同时，梯度消失/爆炸问题也随之出现，但是随着归一地初始化以及在网络中间层进行归一化等等方式的出现，反向传播的梯度下降又变得可行起来。

但是呢，有一个问题出现了，见下图：

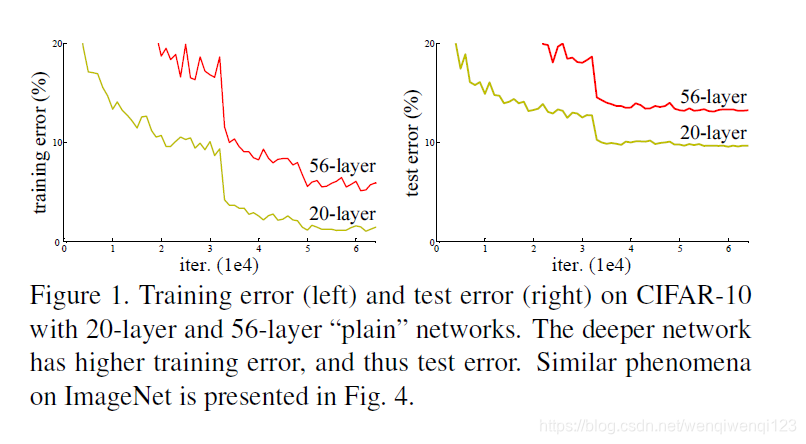
图中56层的‘plain’网络，即56层全连接网络，不仅是测试误差，它的训练误差也比20层的网络高！那么这就不是一个过拟合问题了，因为如果是过拟合的话，训练时误差应该很低而测试时很高。而图中是无论训练还是测试都更高。

我们试想一下，假设有两个网络，三层和五层网络，我们最终要得到的结果是1。如果三层网络就可以输出1，那么五层网络只要在最后两层做一个恒等变换，文中叫“ ”，便也可以得到1。因此理论上五层网络绝对不应该比三层网络差的，但是呢实验结果表明，这多出来的网络层并不能做到这种恒等变换。因此在这篇文章中，何恺明给出了解决方法，见下图：

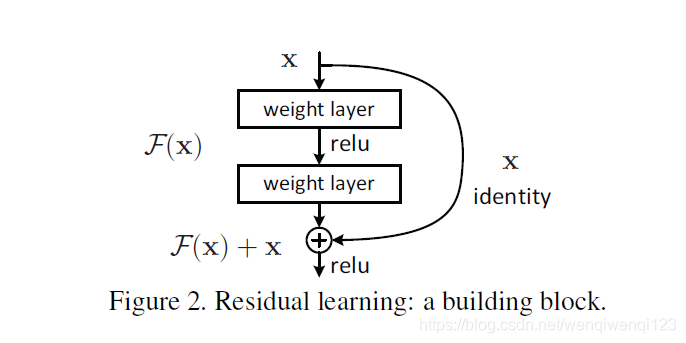
设网络输入为x，经过几层网络的输出为F（x），而要传给下层网络的输入为H（x），右边那条路叫做（捷径）。

在正常的网络中，应该传递给下一层网络的输入是

H（x）=F（x）

但在中，传递给下一层的输入变为

H（x）=F（x）+x

这样网络会比之前的方式更容易优化。试想极端情况，这几层网络完全是多余的，那么在正常的网络中，这几层网络就要努力做到恒等变换，使得

H（x）=F（x）=x

而在中，只需要把F（x）变为0即可，输出变为

H（x）=F（x）+x=0+x=x

很明显，将网络的输出优化为0比将其做一个恒等变换要容易得多。

于是乎，的核心公式如下：

其中Ws是一个矩阵。当然作者也指出实验证明了对于同等维度的变换不需要用到Ws，只需要在维度不一致的情况下使用Ws来统一维度即可。而且此网络结构完全适用于CNN。

整个的结构对比图如下：

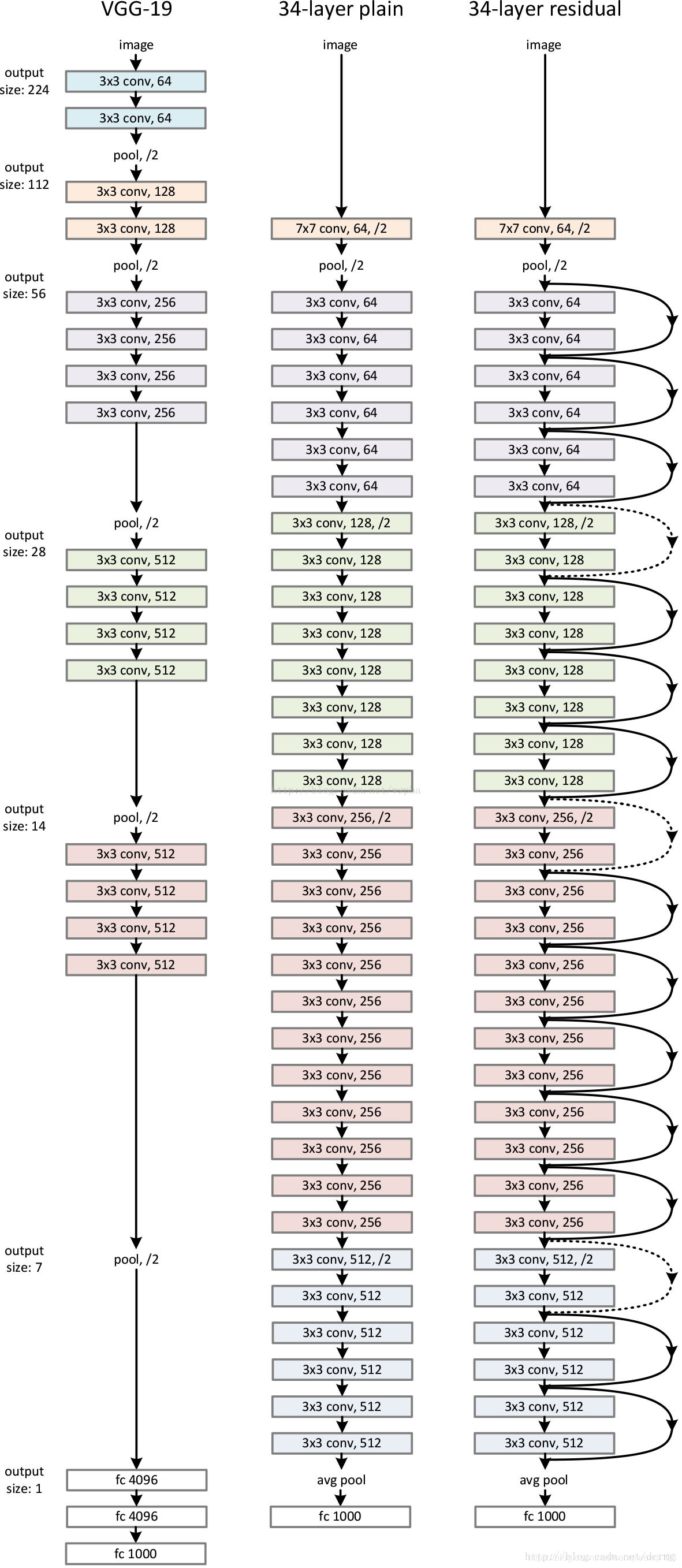
以及各个层数的详细结构表：

当然啦作者还做了个对比实验：

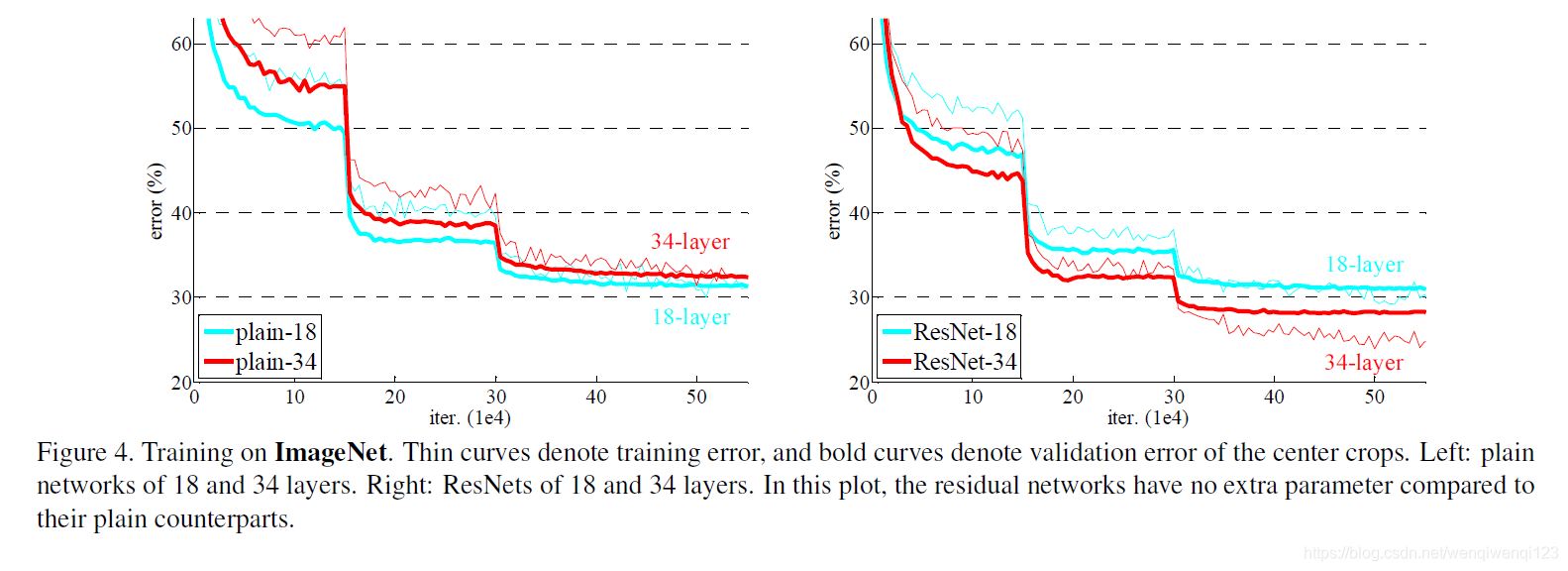
上图左边是plain ，加了BN（batch ）来训练以防止梯度消失。而右边是的结果。可以看出对于普通网络，更深的网络训练误差不一定更低，而有效地克服了这个问题。而且并没有增大网络的参数。

值得一提的是，由于在F（x）+x的时候会有维度不一致的问题，作者在这里提出了三种的方式。A、升维的时候直接用（与前面的图一样，没有多余参数） B、升维的时候用1*1的卷积层来进行升维 C、在所有中使用1*1卷积。

结果自然是C最好，但是因为C的结果只好了一点点，但是参数多了很多，所以并没有被采用（结果好的原因只是因为参数变多了而已）。而A的方式因为相比普通网络完全没有增多参数，且结果也相当不错得到了采用。

在实验部分作者跑了许多实验，当然结果都是为了说明非常牛逼，这里就不做过多的介绍了。感兴趣的朋友请看看原文吧。比较惹人注意的是1000+层的网络出现了过拟合，结果并没有比100+的网络更好。